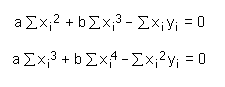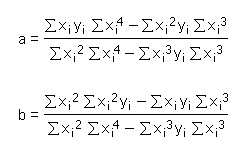Univariate Regression - Derivation of Equations

The principle of this derivation is quite simple: the least squares regression curve is one that minimizes the sum of squared differences between the estimated and the actual y values for given x values (residuals). Therefore you first have to define the equation of the sum of squares, calculate the partial derivatives (with respect to each parameter), and equate them to zero. The rest is just plain algebra to obtain an expression for the parameters.

Let us conduct this procedure for a particular example:

This formula is to be estimated from a series of data points [x_i,y_i], where the x_i are the independent values, and the y_i are to be estimated. By substituting the y_i values with their estimates ax_i+bx_i² we obtain the following series of data points: [xi, ax_i+bx_i²]. The actual values of the y values are, however, the y_i. Thus the sum of squared errors S for n data points is defined by

Now we have to calculate the partial derivatives with respect to the parameters a and b, and equate them to zero:

These two equations can easily be reduced by introducing the sums of the individual terms:

Now, solve these equations for the coefficients a and b:

And then substitute the expressions for a and b into their counterparts, with the following final results: