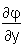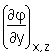Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.

Home Math Background Varia Partial Derivative
See also: Error Propagation 

Partial Derivative

Unter einer partiellen Ableitung versteht man die Ableitung einer Funktion mehrerer Variablen f(x1,...xn) bei der alle Variablen bis auf die abgeleitete konstant gehalten werden. Solche partielle Ableitungen haben einen vielfältigen Anwendungsbereich, von der Vector-Algebra bis zur Differentialgeometrie.

Man schreibt eine partielle Ableitung mit dem Symbol . Dieses Symbol ist gleich dem kursiven "d" der cyrillischen Schrift (eingeführt wurde das Sysmbol von Legendre). Möchte man ausdrücken, dass man eine Funktion φ nach einer bestimmten Variablen (z.B. y) partiell differenziert, so schreibt man das in folgender Form an:

Möchte man speziell darauf hinweisen, welche Variablen konstant gehalten werden, so kann man das durch Aufzählung der konstanten Variablen außerhalb einer runden Klammer machen. Angenommen die Funktion φ(x,y,z) soll nach y partiell differenziert werden, so kann man optional die Variablen x und z außerhalb der Klammer anschreiben:

Die Regeln für die Bildung der partiellen Ableitung sind exakt gleich zu den Regeln für die "normale" Ableitung, nur dass man alle konstanten Variablen auch formal als Konstante behandelt (das heisst, Terme, die nur konstante Variable enthalten, "verschwinden" beim Differenzieren).

Beispiel:

Betrachten wir einen Kegel, so wissen wir, dass das Volumen V des Kegels durch folgende Funktion bestimmt ist:

V = V(r,h) = r2hπ/3.

Nehmen wir an, dass wir die Höhe des Kegels konstant halten und nur dessen Radius ändern. Wenn wir die Änderung des Kegelvolumens in Abhängigkeit vom Radius wissen möchten, brauchen wir nur die partielle Ableitung nach r bilden:

Umgekehrt kann man natürlich auch die Frage stellen, wie sich das Volumen des Kegels ändert, wenn man den Radius konstant hält und nur die Höhe ändert:

Das Volumen ändert sich also bei Änderung der Höhe um eine Längeneinheit um r2π/3.
Home Math Background Varia Partial Derivative