Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu.

Home Statistische Tests Grundlagen Signifikanzniveau
Siehe auch: Verteilungen - Einführung, Der Begriff 'signifikant', Effektgröße 
 
Search the VIAS Library  |  Index


Signifikanzniveau

Author: Hans Lohninger

Bei der Beobachtung von Zufallsprozessen gibt es immer eine gewisse Wahrscheinlichkeit, dass die Ergebnisse einen bestimmten Grenzwert überschreiten. Die Wahrscheinlichkeit der Überschreitung dieses Grenzwerts wird als Signifikanzniveau α bezeichnet. Man sagt auch "das Ergebnis ist signifikant". (1) Dieser Ausdruck kommt aus der Theorie der statistischen Tests, in der die berechnete Testgröße als Zufallsvariable aufgefasst wird. Überschreitet die Testgröße den Grenzwert zx (die kritische Grenze), dann ist die Wahrscheinlichkeit einen Fehler 1. Art zu machen kleiner als das Signifikanzniveau α.

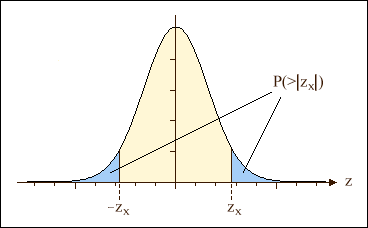
Der eingefärbte Bereich in der obigen Dichteverteilung drückt die Wahrscheinlichkeit aus, mit der das Ergebnis z eines Experiments den Grenzwert zx überschreitet. In manchen Fällen kann sich die gestellte Frage implizit auf zwei Grenzwerte beziehen, wie in der unteren Abbildung zu sehen ist:

In diesem Fall ist das Signifikanzniveau die Summe der Bereiche unter -zx und über +zx.

Kritische Grenzen - der Vergleich von Äpfel und Birnen.


(1) In der statistischen Literatur liest man gelegentlich die Bezeichungen "nicht signifikant", "hoch signifikant", oder ähnliches. Diese Bezeichnungen beziehen sich immer auf das Signifikanzniveaus eines Tests, dabei hat sich folgende Übereinkunft herausgebildet:
α > 0.05 (> 5%) .... nicht signifikant
α = 0.01 bis 0.05 (1 bis 5%) .... signifikant
α = 0.001 bis 0.01 (0.1 bis 1%) .... hoch signifikant
α ≤ 0.001 (≤ 0.1%) .... höchst signifikant (schlüssig)

Home Statistische Tests Grundlagen Signifikanzniveau

Last Update: 2013-11-10