Vektor-Operatoren

Author: Hans Lohninger

Nablaoperator

Der Nablaoperator ist ein vektorieller Differentialoperator für den gilt: = i +j +k, wobei i, j, und k die Einheitsvektoren des Koordinatensystems sind. Die Anwendung des Nablaoperators auf ein Skalarfeld ergibt den Gradienten, das skalare Produkt mit einem Vektorfeld ergibt die Divergenz, und das Vektorprodukt die Rotation. Die Bezeichnung Nabla entspringt der Ähnlichkeit des Operators zu einem hebräischen Saiteninstrument, das etwa die Form des Zeichens hat.

Gradient

Ist φ = φ(x,y,z) eine skalare Ortsfunktion, so ist der Gradient von φ in kartesischen Koordinaten gleich dem inneren (skalaren) Produkt des Nablaoperators mit der Ortsfunktion: grad φ = φ = i +j +k Der Gradient weist in die Richtung der stärksten Steigung der Ortsfunktion, sein Betrag gibt die "Steilheit" der Ortsfunktion an der betreffenden Stelle an.

Divergenz

Ist v(r) ein differenzierbares stetiges Vektorfeld, so ist die Divergenz gleich dem skalaren Produkt des Nablaoperators mit dem Vektor v: div v = v = + + 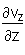Die Divergenz gibt die Quellenergiebigkeit (Überschuss) eines Einheitsvolumens an (Differenz zwischen einströmendem und ausströmendem Vektorfluss durch die Umrandung des Volumens).

Rotation

Ist v(r) ein differenzierbares stetiges Vektorfeld, so ist die Rotation gleich dem Vektorprodukt des Nablaoperators mit dem Vektor v: Die Rotation beschreibt die Wirbel des Vektorfeldes v und ist ein Maß für die Queränderungen eines Vektorfeldes (z.B. entlang der geschlossenen kreisförmigen magnetischen Feldlinien um einen elektrischen Leiter).

Laplace-Operator

Der Laplace-Operator stellt eine Kombination von Divergenz und Gradient dar und wird durch das Symbol Δ bezeichnet. Für kartesische Koordinaten gilt: Anmerkung: Bei Anwendung auf vektorielle Funktionen muss man die Beziehung div grad = grad div - rot rot verwenden.