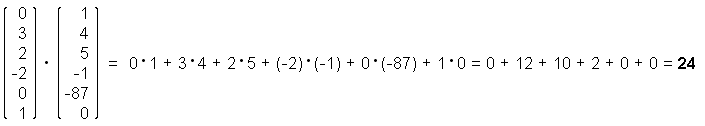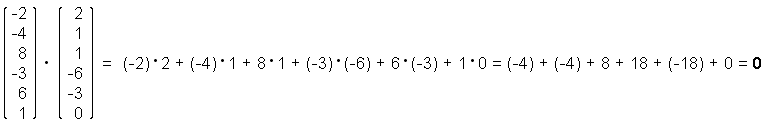Inner Product of Two Vectors

Inner product

Let ak and bk be two arbitrary vectors of the same order, and p an arbitrary scalar from the vector's basic set. Then, the inner product p := ab is calculated by calculating the sum of the element-wise productsp := a1b1 + a2b2 + ... + akbk

The fact that the inner product of two vectors result in a scalar rather than in a vector sometimes gives rise to mistakes. The inner product is occasionally called a "scalar product", which should be avoided in order to not mix up the inner product and the multiplication of a vector by a scalar. Another name for the inner product is a "dot product".

Examples: