Vector Operators

Del operator

The del operator (not to be mixed up with the delta operator) is a differential operator which is defined as follows: = i +j +k, where i, j, and k are the unit vectors of the coordinate system. The application of the del operator on a scalar field results in the gradient, the dot product with a vector field yields the divergence, and the vector product with a vector field results in the curl.

Gradient

if φ = φ(x,y,z) is a scalar function then the gradient of φ in a Cartesian coordinate system is equal to the scalar product of the del operator and the function φ: grad φ = φ= i +j +k The gradient points in the direction of the steepest descent of the function, its absolute value specifies the slope of the function at a particular location.

Divergence

If the vector field v(r) is continuous and differentiable then the divergence is equal to dot product of the del operator and the vector v: div v = .v = + + The divergence defines the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. It measures the magnitude of the vector field's source at this particular point.

Curl	If the vector field v(r) is continuous and differentiable then the curl is equal to the vector product of the del operator and the vector v: The length and direction of the curl (which is a vector) characterize the rotation at that point.

Laplacian operator

The Laplacian operator is a combination of divergence and gradient and is denoted by the symbol Δ. For a Cartesian coordinate system the following equation holds: 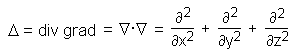Hint: in order to apply the Laplacian to vector functions the following equality may be utilized: div grad = grad div - rot rot.