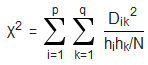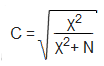Kontingenzkoeffizient

Author: Hans Lohninger

Betrachten wir die Kontingenztafel für zwei nominal skalierte Variablen, so können wir die Häufigkeit des Auftretens einer Merkmalskombination h_ij bei unkorrelierten Variablen berechnen mit:

h_ik = h_ih_k/N

Tritt eine Korrelation auf, so werden die tatsächlichen Häufigkeiten H_ik von den idealen unkorrelierten Häufigkeiten h_ik abweichen. Die Differenz D_ik zwischen unkorrelierter und tatsächlicher Häufigkeit ergibt sich somit aus

D_ik = H_ik - h_ik = H_ik - h_ih_k/N

Für unkorrelierte Variablen muss die diese Differenz für jede Zelle jeweils um null herum liegen. Eine Aussage über die Korrelation lässt sich nun treffen wenn man die Häufigkeitsdifferenzen quadriert und aufsummiert und jeweils zu den Idealwerten in Relation setzt:

Dieser χ²-Koeffizient hat allerdings den gravierenden Nachteil, dass der Wert von der Dimension der Kontingenztabelle und vom Stichprobenumfang abhängt. Um die Abhängigkeit vom Stichprobenumfang zu eliminieren, wird der Kontingenzkoeffizient C nach Pearson wie folgt definiert:

Hinweis:

Im Gegensatz zum Korrelationskoeffizienten gibt der (korrigierte) Kontingenzkoeffizient nicht die Richtung der Korrelation an, sondern nur die Stärke des Zusammenhangs.