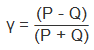Goodman and Kruskal's Gamma

Author: Hans Lohninger

Goodman und Kruskal's Gamma (oder schlicht Gamma) ist ein symmetrisches Maß der Assoziation (Korrelation), das Werte im Bereich von -1.0 bis +1.0 liefert. The Idee hinter Gamma besteht darin, die relative Differenz zwischen konkordanten und diskordanten Paaren⁽¹⁾ in einer sortierten Liste von gepaarten Beobachtungen zu bestimmen (wobei Bindungen ignoriert werden).

Wenn man die Zahl der konkordanten Paare mit P und die Zahl der diskordanten Paare mit Q bezeichnet, so errechnet sich Gamma nach folgender Formel:

Goodman und Kruskal's Gamma ist für große Stichproben angenähert normalverteilt, so dass man p-Werte bzw. Signifikanzniveaus berechnen kann.

Vorsicht:

Ein Wert von null für Gamma bei nicht-dichotomen Variablen heisst nicht notwendigerweise, dass es keine Korrelation zwischen den zwei Variablen gibt. Umgekehrt haben zwei unkorrelierte Variablen immer einen Gamma-Wert von null.

(1)	Konkordante bzw. diskordante Paare sind folgendermaßen definiert: Wenn wir die x/y-Paare nach x in aufsteigender Reihenfolge sortieren und ein bestimmtes Paar betrachten, dann spricht man von einem konkordanten Paar falls der y-Wert dieses Paars größer als der y-Wert des vorhergehenden Paars ist, und von einem diskordanten Paar falls das nicht der Fall ist.